|
| 1 | +# 1761. Minimum Degree of a Connected Trio in a Graph |
| 2 | + |
| 3 | +- Difficulty: Hard. |
| 4 | +- Related Topics: Graph. |
| 5 | +- Similar Questions: Add Edges to Make Degrees of All Nodes Even. |
| 6 | + |
| 7 | +## Problem |
| 8 | + |
| 9 | +You are given an undirected graph. You are given an integer `n` which is the number of nodes in the graph and an array `edges`, where each `edges[i] = [ui, vi]` indicates that there is an undirected edge between `ui` and `vi`. |
| 10 | + |
| 11 | +A **connected trio** is a set of **three** nodes where there is an edge between **every** pair of them. |
| 12 | + |
| 13 | +The **degree of a connected trio** is the number of edges where one endpoint is in the trio, and the other is not. |
| 14 | + |
| 15 | +Return **the **minimum** degree of a connected trio in the graph, or** `-1` **if the graph has no connected trios.** |
| 16 | + |
| 17 | + |
| 18 | +Example 1: |
| 19 | + |
| 20 | +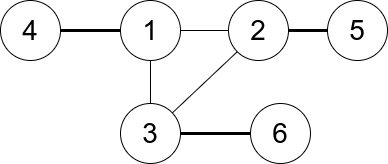 |
| 21 | + |
| 22 | +``` |
| 23 | +Input: n = 6, edges = [[1,2],[1,3],[3,2],[4,1],[5,2],[3,6]] |
| 24 | +Output: 3 |
| 25 | +Explanation: There is exactly one trio, which is [1,2,3]. The edges that form its degree are bolded in the figure above. |
| 26 | +``` |
| 27 | + |
| 28 | +Example 2: |
| 29 | + |
| 30 | +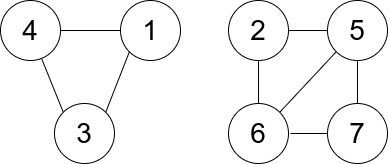 |
| 31 | + |
| 32 | +``` |
| 33 | +Input: n = 7, edges = [[1,3],[4,1],[4,3],[2,5],[5,6],[6,7],[7,5],[2,6]] |
| 34 | +Output: 0 |
| 35 | +Explanation: There are exactly three trios: |
| 36 | +1) [1,4,3] with degree 0. |
| 37 | +2) [2,5,6] with degree 2. |
| 38 | +3) [5,6,7] with degree 2. |
| 39 | +``` |
| 40 | + |
| 41 | + |
| 42 | +**Constraints:** |
| 43 | + |
| 44 | + |
| 45 | + |
| 46 | +- `2 <= n <= 400` |
| 47 | + |
| 48 | +- `edges[i].length == 2` |
| 49 | + |
| 50 | +- `1 <= edges.length <= n * (n-1) / 2` |
| 51 | + |
| 52 | +- `1 <= ui, vi <= n` |
| 53 | + |
| 54 | +- `ui != vi` |
| 55 | + |
| 56 | +- There are no repeated edges. |
| 57 | + |
| 58 | + |
| 59 | + |
| 60 | +## Solution |
| 61 | + |
| 62 | +```javascript |
| 63 | +/** |
| 64 | + * @param {number} n |
| 65 | + * @param {number[][]} edges |
| 66 | + * @return {number} |
| 67 | + */ |
| 68 | +var minTrioDegree = function(n, edges) { |
| 69 | + var { map, lenMap } = buildMap(n, edges); |
| 70 | + var res = Number.MAX_SAFE_INTEGER; |
| 71 | + for (var i = 0; i < map.length; i++) { |
| 72 | + var arr = Object.keys(map[i]); |
| 73 | + for (var j = 0; j < arr.length; j++) { |
| 74 | + var m = arr[j]; |
| 75 | + if (m < i) continue; |
| 76 | + for (var k = j + 1; k < arr.length; k++) { |
| 77 | + var n = arr[k]; |
| 78 | + if (n < i) continue; |
| 79 | + if (map[m][n]) { |
| 80 | + res = Math.min( |
| 81 | + res, |
| 82 | + arr.length - 2 + lenMap[m] - 2 + lenMap[n] - 2, |
| 83 | + ); |
| 84 | + } |
| 85 | + } |
| 86 | + } |
| 87 | + } |
| 88 | + return res === Number.MAX_SAFE_INTEGER ? -1 : res; |
| 89 | +}; |
| 90 | + |
| 91 | +var buildMap = function(n, edges) { |
| 92 | + var map = Array(n + 1).fill(0).map(() => ({})); |
| 93 | + var lenMap = Array(n + 1).fill(0); |
| 94 | + for (var i = 0; i < edges.length; i++) { |
| 95 | + var [m, n] = edges[i]; |
| 96 | + map[m][n] = 1; |
| 97 | + map[n][m] = 1; |
| 98 | + lenMap[n]++; |
| 99 | + lenMap[m]++; |
| 100 | + } |
| 101 | + return { map, lenMap }; |
| 102 | +}; |
| 103 | +``` |
| 104 | + |
| 105 | +**Explain:** |
| 106 | + |
| 107 | +Brute-force with hashmap. |
| 108 | + |
| 109 | +**Complexity:** |
| 110 | + |
| 111 | +* Time complexity : O(n ^ 3). |
| 112 | +* Space complexity : O(n ^ 2). |
0 commit comments