|
| 1 | +# 2017. Grid Game |
| 2 | +You are given a **0-indexed** 2D array `grid` of size `2 x n`, where `grid[r][c]` represents the number of points at position `(r, c)` on the matrix. Two robots are playing a game on this matrix. |
| 3 | + |
| 4 | +Both robots initially start at `(0, 0)` and want to reach `(1, n-1)`. Each robot may only move to the **right** (`(r, c)` to `(r, c + 1)`) or **down** (`(r, c)` to `(r + 1, c)`). |
| 5 | + |
| 6 | +At the start of the game, the **first** robot moves from `(0, 0)` to `(1, n-1)`, collecting all the points from the cells on its path. For all cells `(r, c)` traversed on the path, `grid[r][c]` is set to `0`. Then, the **second** robot moves from `(0, 0)` to `(1, n-1)`, collecting the points on its path. Note that their paths may intersect with one another. |
| 7 | + |
| 8 | +The **first** robot wants to **minimize** the number of points collected by the **second** robot. In contrast, the **second** robot wants to **maximize** the number of points it collects. If both robots play **optimally**, return *the **number of points** collected by the **second** robot*. |
| 9 | + |
| 10 | +#### Example 1: |
| 11 | +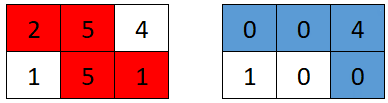 |
| 12 | +<pre> |
| 13 | +<strong>Input:</strong> grid = [[2,5,4],[1,5,1]] |
| 14 | +<strong>Output:</strong> 4 |
| 15 | +<strong>Explanation:</strong> The optimal path taken by the first robot is shown in red, and the optimal path taken by the second robot is shown in blue. |
| 16 | +The cells visited by the first robot are set to 0. |
| 17 | +The second robot will collect 0 + 0 + 4 + 0 = 4 points. |
| 18 | +</pre> |
| 19 | + |
| 20 | +#### Example 2: |
| 21 | +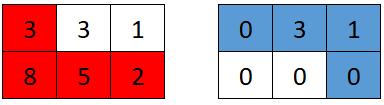 |
| 22 | +<pre> |
| 23 | +<strong>Input:</strong> grid = [[3,3,1],[8,5,2]] |
| 24 | +<strong>Output:</strong> 4 |
| 25 | +<strong>Explanation:</strong> The optimal path taken by the first robot is shown in red, and the optimal path taken by the second robot is shown in blue. |
| 26 | +The cells visited by the first robot are set to 0. |
| 27 | +The second robot will collect 0 + 3 + 1 + 0 = 4 points. |
| 28 | +</pre> |
| 29 | + |
| 30 | +#### Example 3: |
| 31 | +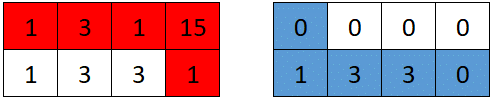 |
| 32 | +<pre> |
| 33 | +<strong>Input:</strong> grid = [[1,3,1,15],[1,3,3,1]] |
| 34 | +<strong>Output:</strong> 7 |
| 35 | +<strong>Explanation:</strong> The optimal path taken by the first robot is shown in red, and the optimal path taken by the second robot is shown in blue. |
| 36 | +The cells visited by the first robot are set to 0. |
| 37 | +The second robot will collect 0 + 1 + 3 + 3 + 0 = 7 points. |
| 38 | +</pre> |
| 39 | + |
| 40 | +#### Constraints: |
| 41 | +* `grid.length == 2` |
| 42 | +* `n == grid[r].length` |
| 43 | +* <code>1 <= n <= 5 * 10<sup>4</sup></code> |
| 44 | +* <code>1 <= grid[r][c] <= 10<sup>5</sup></code> |
| 45 | + |
| 46 | +## Solutions (Rust) |
| 47 | + |
| 48 | +### 1. Solution |
| 49 | +```Rust |
| 50 | +impl Solution { |
| 51 | + pub fn grid_game(grid: Vec<Vec<i32>>) -> i64 { |
| 52 | + let n = grid[0].len(); |
| 53 | + let mut prefix_sum = vec![0; n]; |
| 54 | + let mut suffix_sum = vec![0; n]; |
| 55 | + let mut ret = i64::MAX; |
| 56 | + |
| 57 | + for i in 1..n { |
| 58 | + prefix_sum[i] = prefix_sum[i - 1] + grid[1][i - 1] as i64; |
| 59 | + suffix_sum[n - 1 - i] = suffix_sum[n - i] + grid[0][n - i] as i64; |
| 60 | + } |
| 61 | + |
| 62 | + for i in 0..n { |
| 63 | + ret = ret.min(prefix_sum[i].max(suffix_sum[i])); |
| 64 | + } |
| 65 | + |
| 66 | + ret |
| 67 | + } |
| 68 | +} |
| 69 | +``` |
0 commit comments