README.md

1335. Minimum Difficulty of a Job Schedule

You want to schedule a list of jobs in d days. Jobs are dependent (i.e To work on the ith job, you have to finish all the jobs j where 0 <= j < i).

You have to finish at least one task every day. The difficulty of a job schedule is the sum of difficulties of each day of the d days. The difficulty of a day is the maximum difficulty of a job done on that day.

You are given an integer array jobDifficulty and an integer d. The difficulty of the ith job is jobDifficulty[i].

Return the minimum difficulty of a job schedule. If you cannot find a schedule for the jobs return -1.

Example 1:

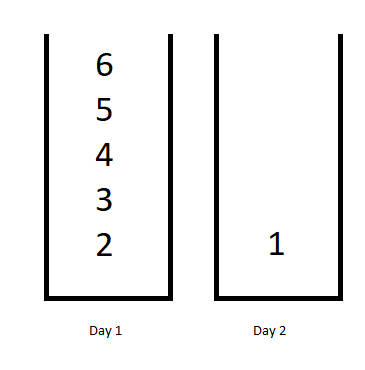
Input: jobDifficulty = [6,5,4,3,2,1], d = 2
Output: 7
Explanation: First day you can finish the first 5 jobs, total difficulty = 6.
Second day you can finish the last job, total difficulty = 1.
The difficulty of the schedule = 6 + 1 = 7

Example 2:

Input: jobDifficulty = [9,9,9], d = 4
Output: -1
Explanation: If you finish a job per day you will still have a free day. you cannot find a schedule for the given jobs.

Example 3:

Input: jobDifficulty = [1,1,1], d = 3
Output: 3
Explanation: The schedule is one job per day. total difficulty will be 3.

Constraints:

• 1 <= jobDifficulty.length <= 300
• 0 <= jobDifficulty[i] <= 1000
• 1 <= d <= 10

Solutions (Rust)

1. Solution

impl Solution {
    pub fn min_difficulty(job_difficulty: Vec<i32>, d: i32) -> i32 {
        let n = job_difficulty.len();
        let d = d as usize;

        if n < d {
            return -1;
        }

        let mut dp = vec![vec![i32::MAX; n + 1]; d + 1];
        let mut max_difficulty = 0;

        for i in 0..=n - d {
            max_difficulty = max_difficulty.max(job_difficulty[i]);
            dp[1][i + 1] = max_difficulty;
        }

        for i in 1..d {
            for j in i..=n + i - d {
                max_difficulty = 0;

                for k in 1..=n + i + 1 - j - d {
                    max_difficulty = max_difficulty.max(job_difficulty[j + k - 1]);
                    dp[i + 1][j + k] = dp[i + 1][j + k].min(dp[i][j] + max_difficulty);
                }
            }
        }

        dp[d][n]
    }
}