|
| 1 | +# 2050. Parallel Courses III |
| 2 | + |
| 3 | +- Difficulty: Hard. |
| 4 | +- Related Topics: Array, Dynamic Programming, Graph, Topological Sort. |
| 5 | +- Similar Questions: Course Schedule III, Parallel Courses, Single-Threaded CPU, Process Tasks Using Servers, Maximum Employees to Be Invited to a Meeting. |
| 6 | + |
| 7 | +## Problem |
| 8 | + |
| 9 | +You are given an integer `n`, which indicates that there are `n` courses labeled from `1` to `n`. You are also given a 2D integer array `relations` where `relations[j] = [prevCoursej, nextCoursej]` denotes that course `prevCoursej` has to be completed **before** course `nextCoursej` (prerequisite relationship). Furthermore, you are given a **0-indexed** integer array `time` where `time[i]` denotes how many **months** it takes to complete the `(i+1)th` course. |
| 10 | + |
| 11 | +You must find the **minimum** number of months needed to complete all the courses following these rules: |
| 12 | + |
| 13 | + |
| 14 | + |
| 15 | +- You may start taking a course at **any time** if the prerequisites are met. |
| 16 | + |
| 17 | +- **Any number of courses** can be taken at the **same time**. |
| 18 | + |
| 19 | + |
| 20 | +Return **the **minimum** number of months needed to complete all the courses**. |
| 21 | + |
| 22 | +**Note:** The test cases are generated such that it is possible to complete every course (i.e., the graph is a directed acyclic graph). |
| 23 | + |
| 24 | + |
| 25 | +Example 1: |
| 26 | + |
| 27 | + |
| 28 | + |
| 29 | + |
| 30 | +``` |
| 31 | +Input: n = 3, relations = [[1,3],[2,3]], time = [3,2,5] |
| 32 | +Output: 8 |
| 33 | +Explanation: The figure above represents the given graph and the time required to complete each course. |
| 34 | +We start course 1 and course 2 simultaneously at month 0. |
| 35 | +Course 1 takes 3 months and course 2 takes 2 months to complete respectively. |
| 36 | +Thus, the earliest time we can start course 3 is at month 3, and the total time required is 3 + 5 = 8 months. |
| 37 | +``` |
| 38 | + |
| 39 | +Example 2: |
| 40 | + |
| 41 | +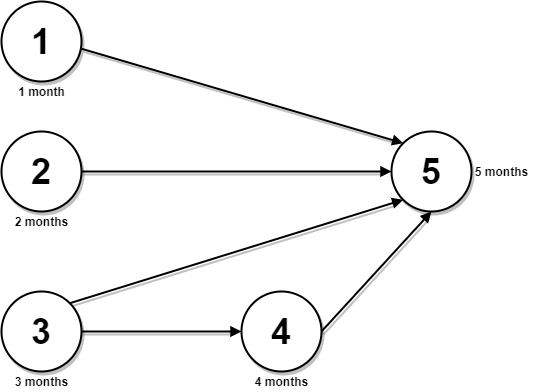 |
| 42 | + |
| 43 | + |
| 44 | +``` |
| 45 | +Input: n = 5, relations = [[1,5],[2,5],[3,5],[3,4],[4,5]], time = [1,2,3,4,5] |
| 46 | +Output: 12 |
| 47 | +Explanation: The figure above represents the given graph and the time required to complete each course. |
| 48 | +You can start courses 1, 2, and 3 at month 0. |
| 49 | +You can complete them after 1, 2, and 3 months respectively. |
| 50 | +Course 4 can be taken only after course 3 is completed, i.e., after 3 months. It is completed after 3 + 4 = 7 months. |
| 51 | +Course 5 can be taken only after courses 1, 2, 3, and 4 have been completed, i.e., after max(1,2,3,7) = 7 months. |
| 52 | +Thus, the minimum time needed to complete all the courses is 7 + 5 = 12 months. |
| 53 | +``` |
| 54 | + |
| 55 | + |
| 56 | +**Constraints:** |
| 57 | + |
| 58 | + |
| 59 | + |
| 60 | +- `1 <= n <= 5 * 104` |
| 61 | + |
| 62 | +- `0 <= relations.length <= min(n * (n - 1) / 2, 5 * 104)` |
| 63 | + |
| 64 | +- `relations[j].length == 2` |
| 65 | + |
| 66 | +- `1 <= prevCoursej, nextCoursej <= n` |
| 67 | + |
| 68 | +- `prevCoursej != nextCoursej` |
| 69 | + |
| 70 | +- All the pairs `[prevCoursej, nextCoursej]` are **unique**. |
| 71 | + |
| 72 | +- `time.length == n` |
| 73 | + |
| 74 | +- `1 <= time[i] <= 104` |
| 75 | + |
| 76 | +- The given graph is a directed acyclic graph. |
| 77 | + |
| 78 | + |
| 79 | + |
| 80 | +## Solution |
| 81 | + |
| 82 | +```javascript |
| 83 | +/** |
| 84 | + * @param {number} n |
| 85 | + * @param {number[][]} relations |
| 86 | + * @param {number[]} time |
| 87 | + * @return {number} |
| 88 | + */ |
| 89 | +var minimumTime = function(n, relations, time) { |
| 90 | + var graph = Array(n).fill(0).map(() => []); |
| 91 | + for (var i = 0; i < relations.length; i++) { |
| 92 | + var [a, b] = relations[i]; |
| 93 | + graph[a - 1].push(b - 1); |
| 94 | + } |
| 95 | + |
| 96 | + var max = 0; |
| 97 | + var dp = Array(n); |
| 98 | + for (var i = 0; i < n; i++) { |
| 99 | + max = Math.max(max, dfs(i, graph, time, dp)); |
| 100 | + } |
| 101 | + return max; |
| 102 | +}; |
| 103 | + |
| 104 | +var dfs = function(i, graph, time, dp) { |
| 105 | + if (dp[i] !== undefined) return dp[i]; |
| 106 | + var max = 0; |
| 107 | + for (var j = 0; j < graph[i].length; j++) { |
| 108 | + max = Math.max(max, dfs(graph[i][j], graph, time, dp)); |
| 109 | + } |
| 110 | + dp[i] = max + time[i]; |
| 111 | + return dp[i]; |
| 112 | +}; |
| 113 | +``` |
| 114 | + |
| 115 | +**Explain:** |
| 116 | + |
| 117 | +nope. |
| 118 | + |
| 119 | +**Complexity:** |
| 120 | + |
| 121 | +* Time complexity : O(n + m). |
| 122 | +* Space complexity : O(n + m). |
0 commit comments