|
| 1 | +# 319. Bulb Switcher |
| 2 | + |
| 3 | +- Difficulty: Medium. |
| 4 | +- Related Topics: Math, Brainteaser. |
| 5 | +- Similar Questions: Bulb Switcher II, Minimum Number of K Consecutive Bit Flips, Number of Times Binary String Is Prefix-Aligned, Find the Pivot Integer. |
| 6 | + |
| 7 | +## Problem |
| 8 | + |
| 9 | +There are `n` bulbs that are initially off. You first turn on all the bulbs, then you turn off every second bulb. |
| 10 | + |
| 11 | +On the third round, you toggle every third bulb (turning on if it's off or turning off if it's on). For the `ith` round, you toggle every `i` bulb. For the `nth` round, you only toggle the last bulb. |
| 12 | + |
| 13 | +Return **the number of bulbs that are on after `n` rounds**. |
| 14 | + |
| 15 | + |
| 16 | +Example 1: |
| 17 | + |
| 18 | +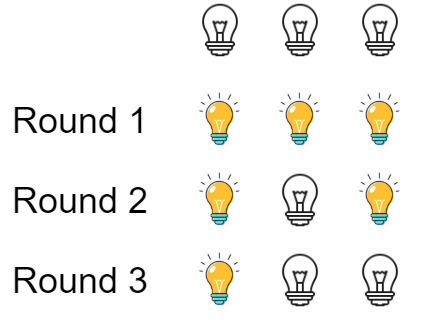 |
| 19 | + |
| 20 | +``` |
| 21 | +Input: n = 3 |
| 22 | +Output: 1 |
| 23 | +Explanation: At first, the three bulbs are [off, off, off]. |
| 24 | +After the first round, the three bulbs are [on, on, on]. |
| 25 | +After the second round, the three bulbs are [on, off, on]. |
| 26 | +After the third round, the three bulbs are [on, off, off]. |
| 27 | +So you should return 1 because there is only one bulb is on. |
| 28 | +``` |
| 29 | + |
| 30 | +Example 2: |
| 31 | + |
| 32 | +``` |
| 33 | +Input: n = 0 |
| 34 | +Output: 0 |
| 35 | +``` |
| 36 | + |
| 37 | +Example 3: |
| 38 | + |
| 39 | +``` |
| 40 | +Input: n = 1 |
| 41 | +Output: 1 |
| 42 | +``` |
| 43 | + |
| 44 | + |
| 45 | +**Constraints:** |
| 46 | + |
| 47 | + |
| 48 | + |
| 49 | +- `0 <= n <= 109` |
| 50 | + |
| 51 | + |
| 52 | + |
| 53 | +## Solution |
| 54 | + |
| 55 | +```javascript |
| 56 | +/** |
| 57 | + * @param {number} n |
| 58 | + * @return {number} |
| 59 | + */ |
| 60 | +var bulbSwitch = function(n) { |
| 61 | + return Math.floor(Math.sqrt(n)); |
| 62 | +}; |
| 63 | +``` |
| 64 | + |
| 65 | +**Explain:** |
| 66 | + |
| 67 | +For the `k`th bulb, it is switched exactly a number of times that is a divisor of `k`. If `k` has an even number of divisors, then the final state of the `k`th light bulb is dark; if `k` has an odd number of divisors, then the final state of the `k`th light bulb is bright. |
| 68 | + |
| 69 | + |
| 70 | +For `k`, if it has divisor `x`, then there must be divisor `k/x`. Therefore, as long as at that time, divisors appear in "pairs". This means that only when `k` is a "perfect square number", it will have an odd number of divisors, otherwise it must have an even number of divisors. |
| 71 | + |
| 72 | +Therefore, we only need to find out the number of perfect square numbers in `1 ~ n`, and the answer is `sqrt(n)` |
| 73 | + |
| 74 | +**Complexity:** |
| 75 | + |
| 76 | +* Time complexity : O(1). |
| 77 | +* Space complexity : O(1). |
0 commit comments